 |
| 【1の解答】 |
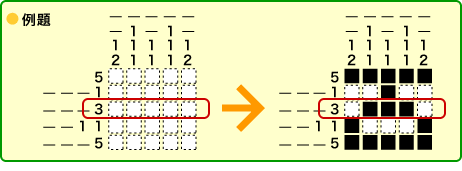
| それぞれの漢字には、人体の一部を表す漢字が含まれています。乱→口、道→首、県→目、挙→手、踏→足。この漢字を、人体に当てはめて上から順に並べると右側のような順になります。 |
【2の解答】 |
| この熟語の読み仮名は、上から読んでも下から読んでも同じです。通して読むと、『いかだなんせんはろうこうろはんせんなだかい』となり、なおかつこの熟語は海や船舶に関係した言葉なので、空欄に当てはまるのは『帆船』と『灘』になります。 |
【3の解答】 |
それぞれ、硬貨や紙幣に描かれているものをあらわしています。(菊→五十円硬貨、桜→百円硬貨、桐→五百円硬貨、鶴→千円札、雉→一万円札)。
なので、ここに当てはまるのは五千円札の『富士』です。(おわび:空欄がひとつしかありませんでした。また、二千円札は除外してあります。) |
【4の解答】 |
| この数字は対応する硬貨の直径の大きさに順に並んでいます。なので、正解は5。 |
【5の解答】 |
| Aさんは午前十時から十五時間寝ており、起きたのは今日の午前一時。『今日』になってから一時間すでに寝てしまっているので、『今日』一睡もしないというのは不可能なのです。 |
【6の解答】 |
| 一手目で前に進むこと。最初の配置で、香車の前は開いていますが、飛車のすぐ前は歩があるため、前に進めないのです。 |
【7の解答】 |
| 三対一。三回目にスタート地点ですれ違ったということは、遅い方の車は一回目はコースの三分の一、二回目にコースの三分の二進み、三回目に一周することになり、早いほうの車はその間三周していることになるから。 |
【8の解答】 |
| トナカイ。トナカイはサンタのそりを引いているので、常にサンタの一歩先にいることになります。 |
【9の解答】 |
| BとC、CとEを押すと左前足が動き、なおかつボタンを二つ同時に押したときには片一方しか反応しないという条件から、Cは左前足だとわかります。同様にして、Aが左後足、Bが右後足、Dは右前足、Eが尻尾だとわかります。 |
【10の解答】 |
| C。五千円札だけしかないとしても、余分に千円を加えなくても済むから。 |
【11の解答】 |
| 飛行機そのもの。 |
【12の解答】 |
| 理容師全員女性なのでした。 |
【13の解答】 |
| まず、ボールを4つずつ3つのグループに分けます。このグループの内2つのグループを選んで、天秤にかけて重さを比べます。ここで、 |
| (i) |
重さが釣り合った場合 |
| |
どちらのグループも同じ重さ、つまり、どちらのボールも重さは同じだと言うことになるので、残る一グループの中に重いボールが入っていることになります。 |
|
| 次に、残った一グループのボールを2つずつのグループに分け、重さを比べ、重かったグループからさらに重いものを選び出せば正解となります。 |
| (ii) |
どちらかが重かった場合 |
| |
重かったグループを(i)と同様にして解けば、どのボールが重いのか分かります。 |
|
【14の解答】 |
| 13.と同様にボールを4つずつ3つのグループに分け、その内2つのグループを選んで、天秤にかけて重さを比べる。 |
| (i) |
つりあった場合 |
| |
左右がつりあった場合、 天秤に乗せていない残りの4個のうちのどれかが重さが違うことがわかる。
よって、そのうちの2個を左側の天秤に乗せ、 つりあっている8個(重さがふつうとわかっている玉)のうちの2つを右側の天秤に乗せる。
そこで、もしつりあっていれば、天秤に乗せたものはどれも 他と同じ重さであることがわかるので、残りの2つのうちのどちらかが答えである。
また、つりあっていなければ、左側に乗せた2個のうちどちらかが、 他と違う重さであることがわかる。
よって、重さが違うかもしれない2個のうち1個を、ふつうの重さであるものと比べ、異なればそれが答え。同じであればもう片方が答えということになる。 (ここで、残りの2つ同士を比べないのは、重さの違う玉は重いのか軽いのかわからないため、天秤が傾くのは当たり前で、だからと言ってどっちがふつうの重さでないかはわからないためである。) |
|
次に、残った一グループのボールを2つずつのグループに分け、重さを比べ、重かったグループからさらに重いものを選び出せば正解となります。 |
| (ii) |
つりあわなかった場合 |
| |
釣り合わなかった場合は、天秤に乗せた8個のうちのどれかが重さが違うことになる。仮に、軽い方の4個を○○○○ 重い方の4個を●●●●として、左右の天秤に、 左:●●○ 右:●●○と乗せる。 |
| (ii-A) |
つりあった場合 |
| |
ここでつりあった場合、8個のうち乗せていない○○のうちどちらかが違う重さであることがわかる。
また、初めに4-4で比べている際に、○は軽いほうであることがわかっている。
よって、○の中のどれかひとつが“重い”ということはありえない。
(どれかひとつが重ければ、他はどれも同じ重さのはずだから、○の方が下に傾くことになる。)
よって、○○のうちどちらかが“軽い”ことがわかる。すなわち、2つの重さを比べて、軽い方が答えとなる。 |
| (ii-B) |
左の方が重い場合 |
| |
この場合、右の○が軽いか、左の●●のうちどちらかが重いかのいずれかになる。それを確かめるためには、左の●●を比べればよい。
(ii-A)と同様の考え方で、●●を比べて傾けば、重い方が答えとなる。
逆に、もしつりあえば、2つは同じ重さであり、また、左の○だけ重いから左に傾くということもありえない。
(○ははじめに軽い方になっているから。)
よって、右の○が答えということになる。 |
| (ii-C) |
右の方が重い場合 |
| |
左右対称なので、(B)と同様にしてできる。
以上より、3回で、玉12個のうちどれが重さが違うかを判断することができる。 |
|